Inspired by the efficient building of the hierarchical model introduced in the textbook Bayesian Data Analysis, our group grew more interest in the flexible usage of RStan. We realized how cumbersome it can be in real-world application if we know the mathematical theory behind the model without a working knowledge in the software. As a result, we decided to explore more on variations in the application of the RStan package for Bayesian models. In addition, we’d like to take advantage of this opportunity to push ourselves one step towards the limits to fortify our understanding of Bayesian statistics. Specifically, we intend to combine the self-motivated study of Rstan with our current knowledge such as linear regression and simulation, which is also what we have been chewing on so-far this semester. From these perspectives, the hierarchical linear regression model is by all means a best choice to focus our attention on.
As for application of this model in real life problem, we decide to study fuel consumption for cars. Nowadays, petroleum consumption of cars is an important question that we pay attention to. In this case, we decide to study the “mtcars” dataset in R that contains some information about fuel consumption and its affected factors. Particularly, we are interested how gross horse power and rear axle ratio affect the miles per gallon for cars.
Hierarchical Linear regression
While the normal linear regression captures only the dependency between the predictors and response, the hierarchical linear regression captures the further inner dependencies using nested groups, namely, hierarchy. These dependencies usually account for the relation among groups and between groups just as the hierarchical model we learned in class. As an easy example, if the original group is student, the higher-order group could be classroom, or even higher: region.
Usually, the hierarchical linear regression contains a 2-level structure, which is also we adopt in this project. Further levels could be considered but not very practical. The inclusion of higher than 2 levels in the hierarchical linear regression is similar to that of making assumptions on prior distributions of the hyper-parameters in the Bayesian context. In the 2-level case, we specify the individual-specific regression coefficients with a joint distribution at level 2. A comparison among different models: no pooling(separate regression without grouping), complete pooling(putting all in one group) and hierarchical(idea of partial pooling, sharing the advantage of both) shows that inappropriate grouping could yield completely opposite result from the truth.
Application using RStan
To implement the theoretical ideas using programming language, RStan provides an efficiently way. As firstly learned from the 8 school hierarchical model demonstration, we outlined the routine program blocks in the “.stan” file as a specified model including all the assumed distributions, supplemented with data(the known values and their respective dimensions) along with parameters (the unknown values involved in the model). In our specific case, a block of transformed parameters is also introduced to make the expressions clearer. On the other hand, the known quantities such as the data as well as the estimates to be directly obtained from them are specified separately in the R environment.
This classification of different quantities into blocks in effect strengthened our understanding of the structure of the model in a comprehensive way. The details of our use of RStan to build the model will be unfolded in the following sections explaining our case of regression model.
Mathematical Background
The illustration of the hierarchical regression model starts with a normal linear regression:
$$Y = \beta_0 + X\beta + r$$ where X is the matrix design of the predictors.
Another convenient way(used in stan.) to represent linear regression is to write the response as a normal random variable, with all the assumptions in the regression coefficients and noise being normal, which is exactly the compact representation in RStan:
$$Y \sim Normal(\beta_0 + X\beta, \sigma^2), \mu= \beta_0 + X\beta$$
In our case, we extend the regression model to have a nested structure to make it a hierarchical linear regression model. That is, we divide the predictors further into several groups and for each group, the coefficients are regressed on (affected by) another set of predictors so that we vary the coefficients by grouping variables:
= dependent variable
= intercept for level-2 unit
= regression coefficient vector associated with X for level-2 unit
r = random error vector associated with level-1 unit nested within the level-2 unit
E(r) = 0; var(r) =
Again, in normal distribution representation, the above can be written as:
$$Y \sim Normal (\beta_0 + X\beta, \sigma^2)$$
$$\beta \sim Normal(\gamma, \tau)$$
Therefore, betas can be simulated from normal distributions with certain correlation structure. In this case, we can study how data affects prior parameters sigma, gamma, and tau as posterior parameters later.
Model Analysis
Step 0. Data and parameters preparation
First install R and optionally RStudio, as a user-friendly environment to use R. Then install the necessary R packages, including rstan package to pass the model file and the data and shinystan package to check the model. The installations using the “install.packages” function are only required the first time you run the code.
library(rstan)
Next, set the working directory to where the stan model is stored and simulate the data.
setwd("C:/Users/SHE3/Desktop/Data")
During the simulation, we first assume that there are 10 types of cars, while for each type of cars there are 50 observations. Therefore, the total number of observations will be 500. For setting up the population level regression coefficients gamma, we use the “mtcars” dataset in R. Then, we run linear regression of miles per gallon(mpg) against gross horse power(hp) and rear axle ratio(drat) as the following:
> fit <- lm(mpg~hp+drat,data=mtcars)
> fit
Call:
lm(formula = mpg ~ hp + drat, data = mtcars)
Coefficients:
(Intercept) hp drat
10.78986 -0.05179 4.69816
> summary(fit)
Call:
lm(formula = mpg ~ hp + drat, data = mtcars)
Residuals:
Min 1Q Median 3Q Max
-5.0369 -2.3487 -0.6034 1.1897 7.7500
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 10.789861 5.077752 2.125 0.042238 *
hp -0.051787 0.009293 -5.573 5.17e-06 ***
drat 4.698158 1.191633 3.943 0.000467 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.17 on 29 degrees of freedom
Multiple R-squared: 0.7412, Adjusted R-squared: 0.7233
F-statistic: 41.52 on 2 and 29 DF, p-value: 3.081e-09
Then we use the coefficients of intercept, hp and drat as the components of gamma. Similarly, we obtain the standard deviation of the group-level coefficient tau by observing the summary of this linear regression model and use the standard error corresponding to each variable (intercept, hp and drat). Finally, for the individual level standard deviation sigma, we observe the standard deviation of the response variable mpg and therefore use that for sigma.
> sd(mtcars$mpg)
[1] 6.026948
The following code shows the simulation process:
#simulate some data
set.seed(20180417)
N<-500 #sample size
J<-10 #number of car types
id<-rep(1:J,each=50) #index of car types
K<-3 #number of regression coefficients
#population-level regression coefficient
gamma<-c(10,-0.05,5)
#standard deviation of the group-level coefficient
tau<-c(5,0.1,1)
#standard deviation of individual observations
sigma<-6
#group-level regression coefficients
beta<-mapply(function(g,t) rnorm(J,g,t),g=gamma,t=tau)
#the model matrix
X<-model.matrix(~x+y,data=data.frame(x=runif(N,-2,2),y=runif(N,-2,2)))
y<-vector(length = N)
for(n in 1:N){
#simulate response data
y[n]<-rnorm(1,X[n,]%*%beta[id[n],],sigma)
}
Step 1. Specify likelihood and prior distributions
As the hierarchical model specified in the mathematical part before, we implement the code in stan as below:
data{int<lower=1>N;//thenumberofobservationsint<lower=1>J;//thenumberofgroupsint<lower=1>K;//numberofcolumnsinthemodelmatrixint<lower=1,upper=J>id[N];//vectorofgroupindicesmatrix[N,K]X;//themodelmatrixvector[N]y;//theresponsevariable}parameters{vector[K]gamma;//population-levelregressioncoefficientsvector<lower=0>[K]tau;//thestandarddeviationoftheregressioncoefficientsvector[K]beta_raw[J];real<lower=0>sigma;//standarddeviationoftheindividualobservations}transformedparameters{vector[K]beta[J];//matrixofgroup-levelregressioncoefficients//computingthegroup-levelcoefficient,basedonnon-centeredparameterizationbasedonsection22.6STAN(v2.12)user's guide
for(j in 1:J){
beta[j] = gamma + tau .* beta_raw[j];
}
}
model {
vector[N] mu; //linear predictor
//priors
gamma ~ normal(0,5); //weakly informative priors on the regression coefficients
tau ~ cauchy(0,2.5); //weakly informative priors, see section 6.9 in STAN user guide
sigma ~ gamma(2,0.1); //weakly informative priors, see section 6.9 in STAN user guide
for(j in 1:J){
beta_raw[j] ~ normal(0,1); //fill the matrix of group-level regression coefficients;
//implies beta~normal(gamma,tau)
}
for(n in 1:N){
mu[n] = X[n] * beta[id[n]]; //compute the linear predictor using relevant group-level regression coefficients
}
//likelihood
y ~ normal(mu,sigma);
}
The first part of the stan code specifies the data, model matrix and response variables. The second part consists of parameters that we use and the transformed version to ensure a more efficient calculation. Here we used non-centered parameterization technique by first defining beta=gamma+tau*beta_raw, then sampling beta as independent unit normal. The third part of the code is the model part, which involves selecting priors for all model parameters.
We chose three weakly informative priors for our parameters, which are normal(0, 5) for gamma (the population level regression coefficients), cauchy(0, 2.5) for tau (the standard deviation of the regression coefficients) and gamma(2,0.1) for sigma (standard deviation of the individual observation). The weakly informative priors are useful because they provide some information on the relative a priori plausibility of the possible parameter values. They also help to reduce posterior uncertainty and stabilize computations.
Step 2. Estimate model parameters
To estimate the model parameters, we computed as below:
By default, the rstan runs 4 Markov chains each with 2000 iterations, half of the iterations are discarded as “warm-up”. The numerical output of the hierarchical model for the “mtcars” sample is shown in below figure:
Inference for Stan model: newmodel.
4 chains, each with iter=2000; warmup=1000; thin=1;
post-warmup draws per chain=1000, total post-warmup draws=4000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
gamma[1] 8.96 0.04 1.22 6.30 8.23 9.02 9.77 11.21 1097 1
gamma[2] -0.14 0.00 0.28 -0.69 -0.32 -0.14 0.04 0.43 3454 1
gamma[3] 4.95 0.01 0.36 4.22 4.73 4.95 5.18 5.64 2188 1
tau[1] 3.55 0.03 0.99 2.14 2.84 3.38 4.05 5.98 1299 1
tau[2] 0.34 0.01 0.28 0.01 0.13 0.29 0.49 1.02 1906 1
tau[3] 0.71 0.01 0.43 0.06 0.41 0.67 0.95 1.64 1445 1
sigma 6.05 0.00 0.19 5.69 5.92 6.05 6.19 6.43 4000 1
Samples were drawn using NUTS(diag_e) at Sat Apr 21 18:08:57 2018.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
Step 3. Check sampling quality
The Rhat and n_eff columns of the table show that R hat is less than 1.1 and the effective sample size is larger than 2000 for all parameters (The code can be revised to have 4000 iterations so that it reaches the standard). To explore the posterior further, we shall employ the use of shinystan package, which is user friendly interface for interactive Markov Chain Monte Carlo diagnostics plots and tables. After installing and loading the package, the user can open the interface website by inputting the following code:
> library(shinystan)
> launch_shinystan(m_hier)
Figure 1 below shows several visual assessments of the population level regression coefficients. There is a table with summary statistics of the selected parameter at the top of the figure. Below the statistics, there is a graph of posterior distribution of the population level regression coefficient (gamma1) on the left. The plot to the right summarizes the autocorrelation as lags increase. The autocorrelation plot shows a high serial correlation persists after several lags, which suggests more samples might be needed to get to a stationary distribution.
Figure 1
The next plot (Figure 2) shows the autocorrelation plot of another population level regression coefficient (gamma 2), which shows a different trend. The correlation is low at the beginning and it goes to zero immediately at lag 1, which means the effective sample size is large.
Figure 2
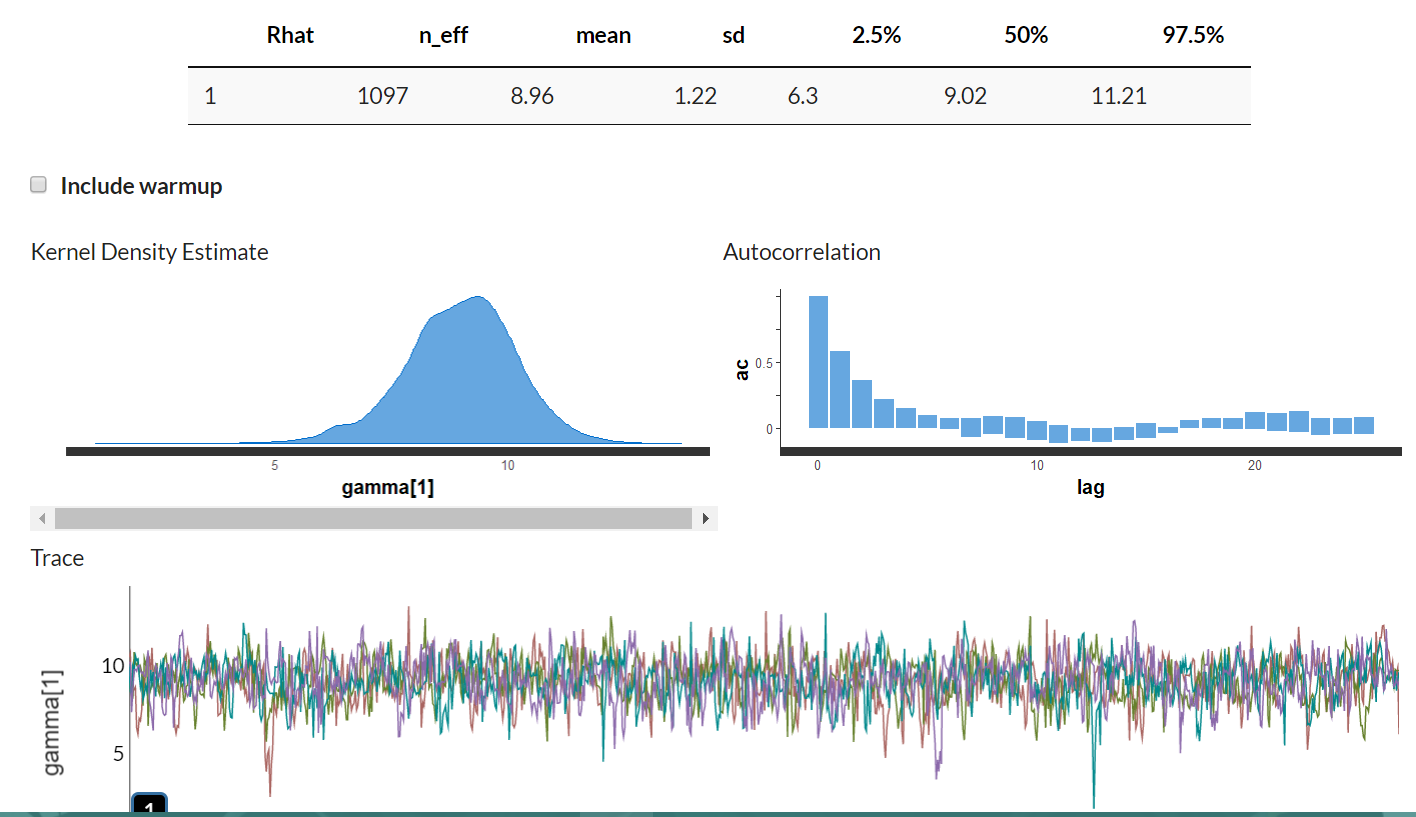
Step 4. Summarize and interpret results
We mainly analyze the results through two ways: point estimates of posterior parameters, posterior intervals (PI) and posterior standard deviation (SD).
A measure of central tendency (mean, median) that chosen to summarize a posterior distribution is a point estimate, which is a single value. In the Bayesian framework, we are interested in the entire posterior distribution rather than the point estimate.
Table 1
Posterior uncertainty intervals describe the range of the model parameters in probabilistic terms. In Table 1, the 2.5% and 97.5% columns show the boundaries of the central 95% intervals for the posterior probability distribution of the parameter. We are 95% confident that the parameter value lies within the 95% posterior intervals. The SD column in Table 1 stands for the posterior standard deviation, which is an alternative summary of the uncertainty around the point estimate.
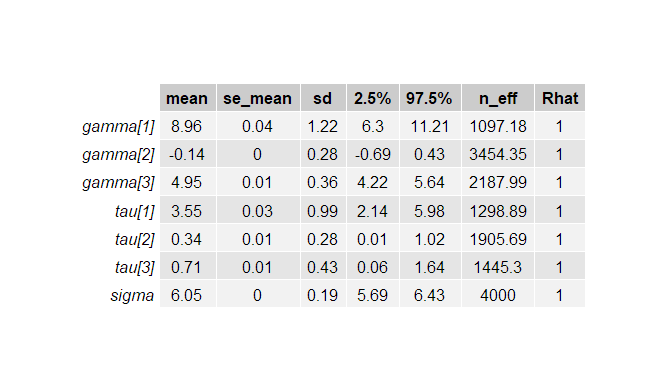
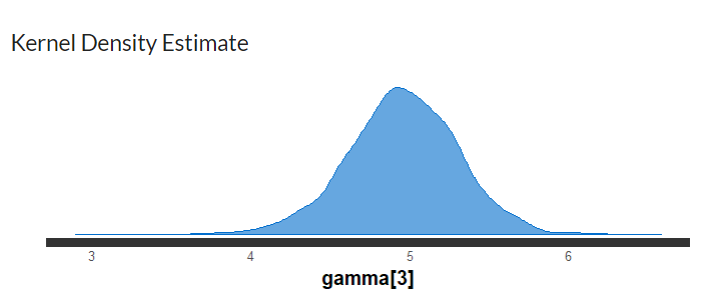
From observing Table 1, the point estimate (in this case which is the mean of the posterior distribution) for the gamma 1 is 8.96, with 95% PI=[6.3,11.21]. The estimate for the population level regression coefficient gamma 3 (which corresponds to rear axle ratio) indicates that a one unit change in rear axle ratio is associated with an increase of 4.95 (95%PI = [4.22,5.64]) in mpg (miles per gallon) value. In Figure 3, the posterior probability distribution plot of the regression coefficient shows that the probability mass for this parameter is on positive values, suggesting that mpg value is remarkably associated with rear axle ratio.
Figure 3
Conclusion
In this project, we use hierarchical model and linear regression to study how gross horse power and rear axle ratio affect miles per gallon for 10 types of cars. Specifically, we use R and stan to do the simulation and computation. We found that rear axle ratio has statistically significant effect on mile per gallon for cars, while gross horse power does not. In addition, we found all posterior parameters convergence.
Discussion
Throughout our exploration of the hierarchical linear regression model with RStan, we came to realize the powerfulness of the hierarchical idea to the seemingly irrelevant problem, which provides us with some food for thought, for example the possible combination of hierarchical model with more sophisticated machine learning methods to yield more consistent and coherent results. Other creative ideas for future application could be nesting within models, compromising between models as the complexity and dimension of the problems grow in an unbounded way.
Particularly, the philosophical concept of compromising between models came into view, though only in a general and inconspicuous way, and for the time being not showing direct helpfulness to applications. For example, the analogy of bayesian philosophy (balancing between prior belief and real data for the estimation of model parameters) and hierarchical models (in the sense of compromising between aggregate and disaggregate models) even in the context of regression has broadened our horizon.
Meanwhile, the smooth implementation and compact representation of the model in RStan demonstrated itself bunches of its advantages such as scalability, efficiency and robustness. Its clear-cut structure also aroused our interest in other possible extensions which have not been carried out in it such as user specific functions and non-conjugate prior, which could be another direction of future research.
Appendix
Contribution Statement
In this project, we choose topic and decided to study hierarchical model together. Then,Huiming Xie wrote the introduction, math and discussion part of the paper. Yang Cai and Rui Hu did the computation and wrote the rest of the paper.
Dataset
We used “mtcars” dataset in R, which is the following:
Muth, Chelsea, et al. “User-Friendly Bayesian Regression Modeling: A Tutorial with Rstanarm and Shinystan.” The Quantitative Methods for Psychology, vol. 14, no. 2, Jan. 2018, pp. 99–119., doi:10.20982/tqmp.14.2.p099.
presents an analysis for the recent 5 years data of 10 companies, Apple, Amazon, Bank of America, Facebook, Google, IBM, JP Morgan, Microsoft, Target and Wal...
